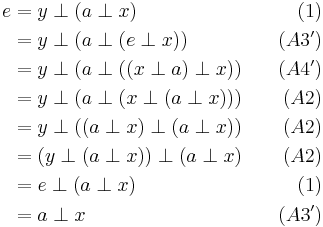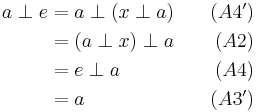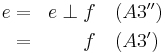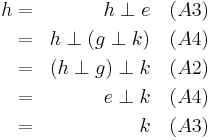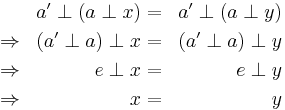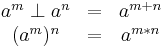Elementary group theory
In mathematics and abstract algebra, a group is the algebraic structure  , where
, where  is a non-empty set and
is a non-empty set and  denotes a binary operation
denotes a binary operation 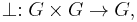 called the group operation. The notation
called the group operation. The notation 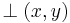 is normally shortened to the infix notation
is normally shortened to the infix notation 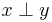 , or even to
, or even to 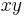 .
.
A group must obey the following rules (or axioms). Let 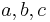 be arbitrary elements of
be arbitrary elements of  . Then:
. Then:
- A1, Closure.
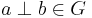 . This axiom is often omitted because a binary operation is closed by definition.
. This axiom is often omitted because a binary operation is closed by definition. - A2, Associativity.
 .
. - A3, Identity. There exists an identity (or neutral) element
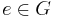 such that
such that 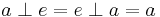 . The identity of
. The identity of  is unique by Theorem 1.4 below.
is unique by Theorem 1.4 below. - A4, Inverse. For each
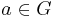 , there exists an inverse element
, there exists an inverse element 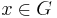 such that
such that 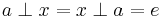 . The inverse of
. The inverse of  is unique by Theorem 1.5 below.
is unique by Theorem 1.5 below.
An abelian group also obeys the additional rule:
- A5, Commutativity.
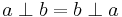 .
.
Contents |
Notation
The group 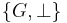 is often referred to as "the group
is often referred to as "the group  " or more simply as "
" or more simply as "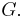 " Nevertheless, the operation "
" Nevertheless, the operation " " is fundamental to the description of the group.
" is fundamental to the description of the group. 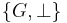 is usually read as "the group
is usually read as "the group  under
under  ". When we wish to assert that
". When we wish to assert that  is a group (for example, when stating a theorem), we say that "
is a group (for example, when stating a theorem), we say that " is a group under
is a group under  ".
".
The group operation  can be interpreted in a great many ways. The generic notation for the group operation, identity element, and inverse of
can be interpreted in a great many ways. The generic notation for the group operation, identity element, and inverse of  are
are 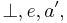 respectively. Because the group operation associates, parentheses have only one necessary use in group theory: to set the scope of the inverse operation.
respectively. Because the group operation associates, parentheses have only one necessary use in group theory: to set the scope of the inverse operation.
Group theory may also be notated:
- Additively by replacing the generic notation by
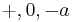 , with "+" being infix. Additive notation is typically used when numerical addition or a commutative operation other than multiplication interprets the group operation;
, with "+" being infix. Additive notation is typically used when numerical addition or a commutative operation other than multiplication interprets the group operation; - Multiplicatively by replacing the generic notation by
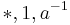 . Infix "*" is often replaced by simple concatenation, as in standard algebra. Multiplicative notation is typically used when numerical multiplication or a noncommutative operation interprets the group operation.
. Infix "*" is often replaced by simple concatenation, as in standard algebra. Multiplicative notation is typically used when numerical multiplication or a noncommutative operation interprets the group operation.
Other notations are of course possible.
Examples
Arithmetic
- Take
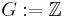 or
or 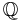 or
or  or
or  , then
, then 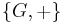 is an abelian group.
is an abelian group. - Take
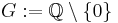 or
or 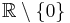 or
or 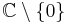 , then
, then 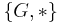 is an abelian group.
is an abelian group.
Function composition
- Let
 be an arbitrary set, and let
be an arbitrary set, and let  be the set of all bijective functions from
be the set of all bijective functions from  to
to  . Let function composition, notated by infix
. Let function composition, notated by infix 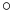 , interpret the group operation. Then
, interpret the group operation. Then 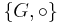 is a group whose identity element is
is a group whose identity element is  The group inverse of an arbitrary group element
The group inverse of an arbitrary group element 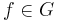 is the function inverse
is the function inverse 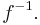
Alternative Axioms
The pair of axioms A3 and A4 may be replaced either by the pair:
- A3’, left neutral. There exists an
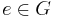 such that for all
such that for all 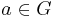 ,
, 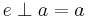 .
. - A4’, left inverse. For each
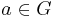 , there exists an element
, there exists an element 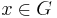 such that
such that 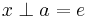 .
.
or by the pair:
- A3”, right neutral. There exists an
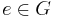 such that for all
such that for all 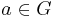 ,
, 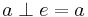 .
. - A4”, right inverse. For each
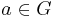 , there exists an element
, there exists an element 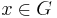 such that
such that 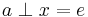 .
.
These evidently weaker axiom pairs are trivial consequences of A3 and A4. We will now show that the nontrivial converse is also true. Given a left neutral element 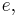 and for any given
and for any given 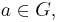 then A4’ says there exists an
then A4’ says there exists an  such that
such that 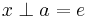 .
.
Theorem 1.2: 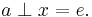
Proof. Let 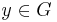 be an inverse of
be an inverse of 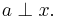 Then:
Then:
This establishes A4 (and hence A4”).
Theorem 1.2a: 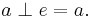
Proof.
This establishes A3 (and hence A3”).
Theorem: Given A1 and A2, A3’ and A4’ imply A3 and A4.
Proof. Theorems 1.2 and 1.2a.
Theorem: Given A1 and A2, A3” and A4” imply A3 and A4.
Proof. Similar to the above.
Basic theorems
Identity is unique
Theorem 1.4: The identity element of a group 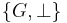 is unique.
is unique.
Proof: Suppose that  and
and  are two identity elements of
are two identity elements of  . Then
. Then
As a result, we can speak of the identity element of 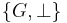 rather than an identity element. Where different groups are being discussed and compared,
rather than an identity element. Where different groups are being discussed and compared, 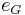 denotes the identity of the specific group
denotes the identity of the specific group 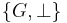 .
.
Inverses are unique
Theorem 1.5: The inverse of each element in 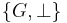 is unique.
is unique.
Proof: Suppose that  and
and  are two inverses of an element
are two inverses of an element  of
of  . Then
. Then
As a result, we can speak of the inverse of an element  , rather than an inverse. Without ambiguity, for all
, rather than an inverse. Without ambiguity, for all  in
in  , we denote by
, we denote by 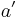 the unique inverse of
the unique inverse of  .
.
Inverting twice takes you back to where you started
Theorem 1.6: For all elements  in a group
in a group 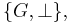
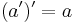 .
.
Proof. 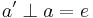 and
and 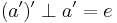 are both true by A4. Therefore both
are both true by A4. Therefore both  and
and 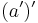 are inverses of
are inverses of 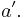 By Theorem 1.5,
By Theorem 1.5, 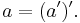
Equivalently, inverting is an involution.
Inverse of ab
Theorem 1.7: For all elements  and
and  in group
in group  ,
, 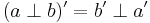 .
.
Proof. 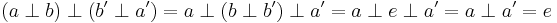 . The conclusion follows from Theorem 1.4.
. The conclusion follows from Theorem 1.4.
Cancellation
Theorem 1.8: For all elements 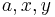 in a group
in a group 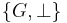 , then
, then 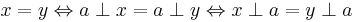 .
.
Proof.
(1) If 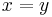 , then multiplying by the same value on either side preserves equality.
, then multiplying by the same value on either side preserves equality.
(2) If 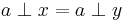 then by (1)
then by (1)
(3) If 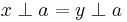 we use the same method as in (2).
we use the same method as in (2).
Latin square property
Theorem 1.3: For all elements 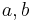 in a group
in a group 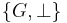 , there exists a unique
, there exists a unique 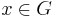 such that
such that 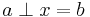 , namely
, namely 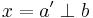 .
.
Proof.
Existence: If we let 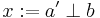 , then
, then 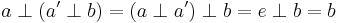 .
.
Unicity: Suppose  satisfies
satisfies 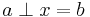 , then by Theorem 1.8,
, then by Theorem 1.8, 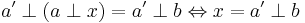 .
.
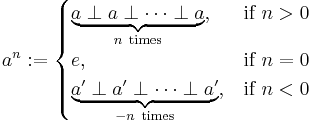
Powers
For 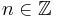 and
and  in group
in group 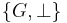 we define:
we define:
Theorem 1.9: For all  in group
in group 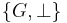 and
and 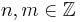 :
:
Order
Of a group element
The order of an element a in a group G is the least positive integer n such that an = e. Sometimes this is written "o(a)=n". n can be infinite.
Theorem 1.10: A group whose nontrivial elements all have order 2 is abelian. In other words, if all elements g in a group G g*g=e is the case, then for all elements a,b in G, a*b=b*a.
Proof. Let a, b be any 2 elements in the group G. By A1, a*b is also a member of G. Using the given condition, we know that (a*b)*(a*b)=e. Hence:
- b*a
- =e*(b*a)*e
- = (a*a)*(b*a)*(b*b)
- =a*(a*b)*(a*b)*b
- =a*e*b
- =a*b.
Since the group operation * commutes, the group is abelian
Of a group
The order of the group G, usually denoted by |G| or occasionally by o(G), is the number of elements in the set G, in which case <G,*> is a finite group. If G is an infinite set, then the group <G,*> has order equal to the cardinality of G, and is an infinite group.
Subgroups
A subset H of G is called a subgroup of a group <G,*> if H satisfies the axioms of a group, using the same operator "*", and restricted to the subset H. Thus if H is a subgroup of <G,*>, then <H,*> is also a group, and obeys the above theorems, restricted to H. The order of subgroup H is the number of elements in H.
A proper subgroup of a group G is a subgroup which is not identical to G. A non-trivial subgroup of G is (usually) any proper subgroup of G which contains an element other than e.
Theorem 2.1: If H is a subgroup of <G,*>, then the identity eH in H is identical to the identity e in (G,*).
Proof. If h is in H, then h*eH = h; since h must also be in G, h*e = h; so by theorem 1.8, eH = e.
Theorem 2.2: If H is a subgroup of G, and h is an element of H, then the inverse of h in H is identical to the inverse of h in G.
Proof. Let h and k be elements of H, such that h*k = e; since h must also be in G, h*h -1 = e; so by theorem 1.5, k = h -1.
Given a subset S of G, we often want to determine whether or not S is also a subgroup of G. A handy theorem valid for both infinite and finite groups is:
Theorem 2.3: If S is a non-empty subset of G, then S is a subgroup of G if and only if for all a,b in S, a*b -1 is in S.
Proof. If for all a, b in S, a*b -1 is in S, then
- e is in S, since a*a -1 = e is in S.
- for all a in S, e*a -1 = a -1 is in S
- for all a, b in S, a*b = a*(b -1) -1 is in S
Thus, the axioms of closure, identity, and inverses are satisfied, and associativity is inherited; so S is subgroup.
Conversely, if S is a subgroup of G, then it obeys the axioms of a group.
- As noted above, the identity in S is identical to the identity e in G.
- By A4, for all b in S, b -1 is in S
- By A1, a*b -1 is in S.
The intersection of two or more subgroups is again a subgroup.
Theorem 2.4: The intersection of any non-empty set of subgroups of a group G is a subgroup.
Proof. Let {Hi} be a set of subgroups of G, and let K = ∩{Hi}. e is a member of every Hi by theorem 2.1; so K is not empty. If h and k are elements of K, then for all i,
- h and k are in Hi.
- By the previous theorem, h*k -1 is in Hi
- Therefore, h*k -1 is in ∩{Hi}.
Therefore for all h, k in K, h*k -1 is in K. Then by the previous theorem, K=∩{Hi} is a subgroup of G; and in fact K is a subgroup of each Hi.
Given a group <G,*>, define x*x as x², x*x*x*...*x (n times) as xn, and define x0 = e. Similarly, let x -n for (x -1)n. Then we have:
Theorem 2.5: Let a be an element of a group (G,*). Then the set {an: n is an integer} is a subgroup of G.
A subgroup of this type is called a cyclic subgroup; the subgroup of the powers of a is often written as <a>, and we say that a generates <a>.
Cosets
If S and T are subsets of G, and a is an element of G, we write "a*S" to refer to the subset of G made up of all elements of the form a*s, where s is an element of S; similarly, we write "S*a" to indicate the set of elements of the form s*a. We write S*T for the subset of G made up of elements of the form s*t, where s is an element of S and t is an element of T.
If H is a subgroup of G, then a left coset of H is a set of the form a*H, for some a in G. A right coset is a subset of the form H*a.
If H is a subgroup of G, the following useful theorems, stated without proof, hold for all cosets:
- And x and y are elements of G, then either x*H = y*H, or x*H and y*H have empty intersection.
- Every left (right) coset of H in G contains the same number of elements.
- G is the disjoint union of the left (right) cosets of H.
- Then the number of distinct left cosets of H equals the number of distinct right cosets of H.
Define the index of a subgroup H of a group G (written "[G:H]") to be the number of distinct left cosets of H in G.
From these theorems, we can deduce the important Lagrange's theorem, relating the order of a subgroup to the order of a group:
- Lagrange's theorem: If H is a subgroup of G, then |G| = |H|*[G:H].
For finite groups, this can be restated as:
- Lagrange's theorem: If H is a subgroup of a finite group G, then the order of H divides the order of G.
- If the order of group G is a prime number, G is cyclic.
See also
References
- Jordan, C. R and D.A. Groups. Newnes (Elsevier), ISBN 0-340-61045-X
- Scott, W R. Group Theory. Dover Publications, ISBN 0-486-65377-3